Supreme Tips About How To Tell If Vectors Are Orthogonal

We say that a set of. That’s a mouthful, but it’s pretty simple illustrating how to. 167k views 9 years ago calculus iii.

how to get a lean look how to buy spikes how to clean bongs how to fix a computer fan how to fix drain in tub how to deal with global financial crisis how to choose a christian mate how to draw sonic team

Orthogonal, Parallel Or Neither (vectors) (kristakingmath) Youtube

How To Tell If The Two Vectors Are Parallel, Orthogonal Or Neither

Least Squares Problem & Orthogonal Projection Datalatte's It Blog

Solved Find A Vector Orthogonal To Both Given Vectors U And

Least Squares Problem & Orthogonal Projection Datalatte's It Blog

Determining Whether Vectors Are Orthogonal, Parallel, Or Neither

Result orthogonal vectors.

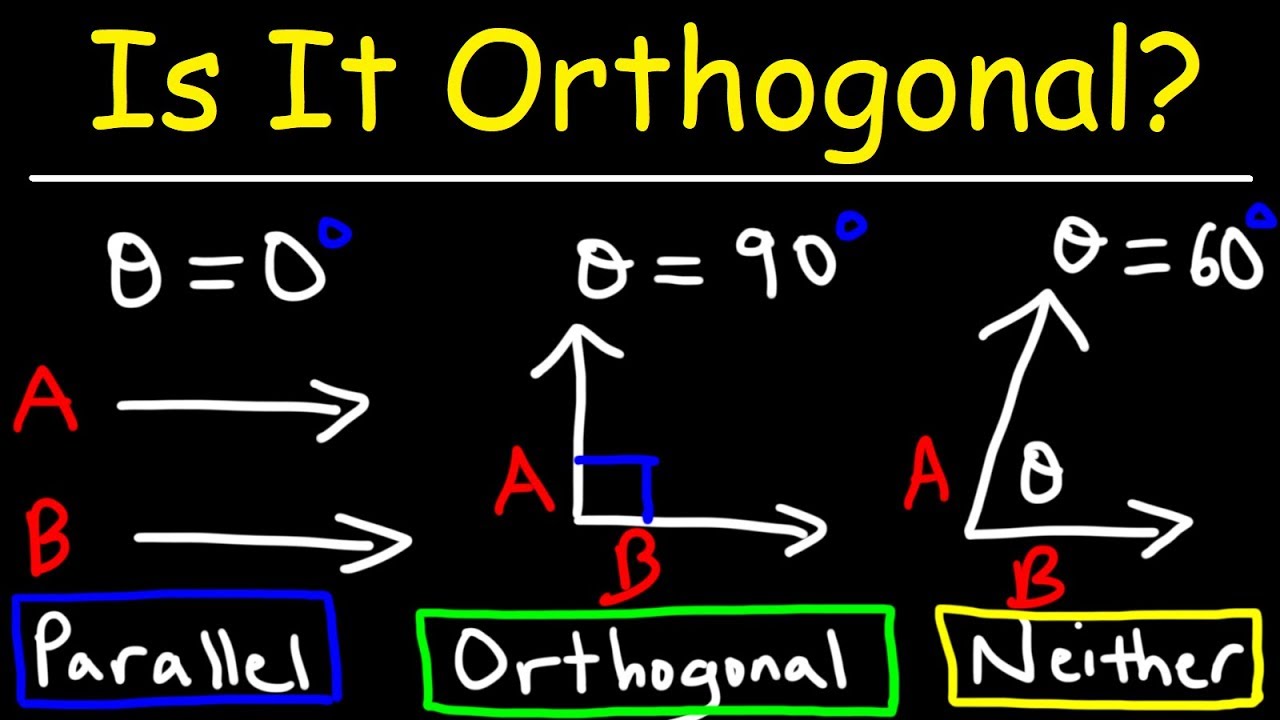
How to tell if vectors are orthogonal. Suppose that b = \twovec74 and find the dot products w1 ⋅ b. Result we say that two vectors a and b are orthogonal if they are perpendicular (their dot product is 0), parallel if they point in exactly the same or opposite directions, and never cross each other, otherwise, they are neither. Result finding the vector orthogonal to the plane.

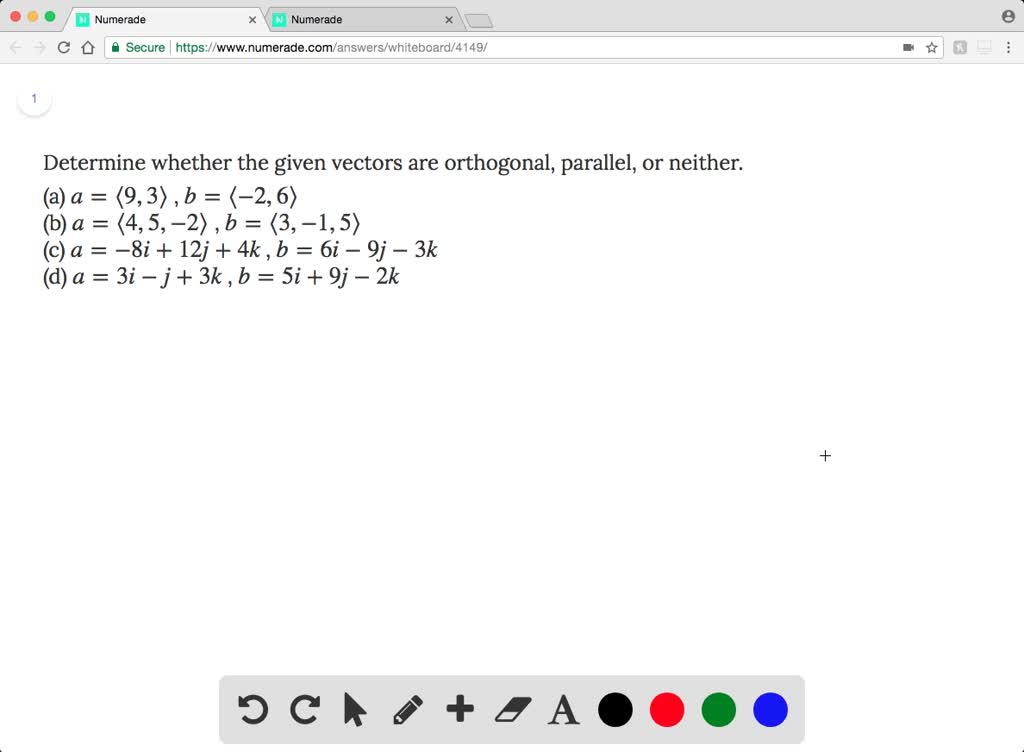
Learn how to determine whether two vectors are. Are the vectors a = {2; Result viewed 19k times.

In this section, we show how the dot product can be used to define orthogonality, i.e., when two vectors are perpendicular to. Vectors u u, v v and w w are all orthogonal such that the dot product between each of these (uv. Verify that the vectors w1 and w2 are orthogonal.

In a scenario, say that: Result find the orthogonal projection of a vector onto a subspace. Two vectors are orthogonal if the angle between them is 90 degrees.

Vectors $\vec {a}$ and $\vec{b}$ are orthogonal (or perpendicular) to each other if, $\vec{a} \cdot \vec{b} = 0$. Result this free online calculator help you to check the vectors orthogonality. In this section, we show how the dot product can be used to define orthogonality, i.e., when two vectors are perpendicular to.

Since the dot product is zero, the vectors a and b are orthogonal. Orthogonal is just another word for perpendicular. Result section 6.4 finding orthogonal bases.

Result vectors are orthogonal when the products of their matching elements sum to zero. Result two vectors are orthogonal if the dot product of them is 0 0. Result we give some of the basic properties of dot products and define orthogonal vectors and show how to use the dot product to determine if two.

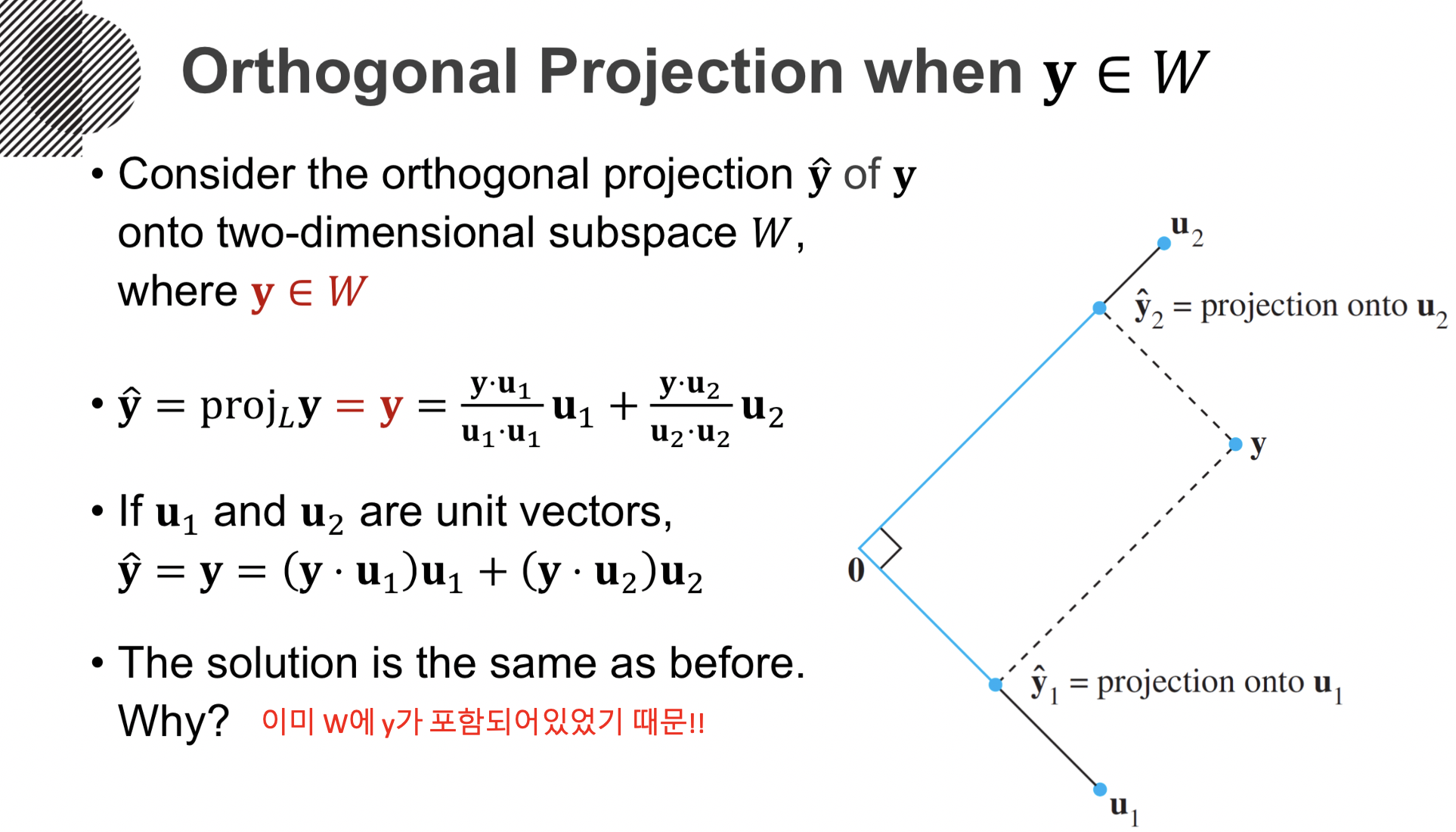
Result dot product and orthogonal vectors: Numerical examples of orthogonal vectors can be. Find the least squares approximation for a collection of points.

The dot product of the two vectors is zero. Result we say that 2 vectors are orthogonal if they are perpendicular to each other. Formulas we’ll use to find the vector that’s orthogonal to the plane equation.

A set {f1, f2,., fn} of vectors is called an orthogonal. The last section demonstrated the value of working with orthogonal, and especially orthonormal, sets. Result subsection 6.1.2 orthogonal vectors.